ত্রিভুজের যেকোনো দুই বাহুর দৈর্ঘ্যের সমষ্টির সাথে তৃতীয় বাহুর দৈর্ঘ্যের সম্পর্ক রয়েছে। সম্পর্কটি অনুধাবনের জন্য দলগতভাবে নিচের কাজটি কর।
কাজ  রুলারের সাহায্যে ত্রিভুজের বাহুগুলোর দৈর্ঘ্য মাপ এবং নিচের সারণিটি পূরণ কর। |
লক্ষ করি, যেকোনো ত্রিভুজের যেকোনো দুই বাহুর দৈর্ঘ্যের যোগফল এর তৃতীয় বাহুর দৈর্ঘ্য অপেক্ষা বেশি। আমরা আরও লক্ষ করি, যেকোনো ত্রিভুজের যেকোনো দুই বাহুর দৈর্ঘ্যের বিয়োগফল এর তৃতীয় বাহুর দৈর্ঘ্য অপেক্ষা কম।
কাজ: নিচের কোন ক্ষেত্রে ত্রিভুজ আঁকা সম্ভব- ব্যাখ্যা দাও।
১। 1 সেমি, 2 সেমি ও 3 সেমি ২। 1 সেমি, 2 সেমি ও 4 সেমি ৩। 4 সেমি, ও সেমি ও 5 সেমি |
ত্রিভুজের যেকোনো দুই বাহুর দৈর্ঘ্যের সমষ্টি এর তৃতীয় বাহুর দৈর্ঘ্য অপেক্ষা বৃহত্তর।
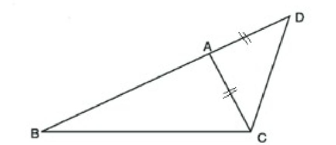
বিশেষ নির্বচন: ধরি ABC -এ BC বৃহত্তম বাহু। প্রমাণ করতে হবে যে (AB + AC) > BC
অঙ্কন: BA কে D পর্যন্ত বর্ধিত করি, যেন AD = AC হয়। C,D যোগ করি।
প্রমাণ:
| ধাপ | যথার্থতা |
(১) ADC - এ AD = AC ∴ ∠ ACD = ∠ ADC : ∠ ACD = ∠ BDC (২) ∠ BCD > ∠ ACD ∴ ∠ BCD > ∠ BDC (৩) BCD এ ∠ BCD> ∠ BDC ∴ BD > BC (৪) কিন্তু BD = AB + AD = AB + AC ∴ (AB + AC) > BC (প্রমাণিত) | [সমদ্বিবাহু ত্রিভুজের ভূমি সংলগ্ন কোণদ্বয় সমান] [কারণ ∠ ACD , ∠ BCD এর একটি অংশ]
[ বৃহত্তর কোণের বিপরীত বাহু বৃহত্তর।] [যেহেতু AC = AD ] |
common.read_more